前言
在深度學習領域,模型量化是一項關鍵的優化技術,它能夠顯著減少模型的儲存空間和計算開銷,同時保持模型性能。量化的本質是將高精度的浮點數(通常是32位浮點數)轉換為低精度的整數(通常是8位整數),這個過程需要在精度和效率之間取得平衡。本文將詳細介紹三種主要的量化方法:對稱量化(Symmetric Quantization)、非對稱量化(Asymmetric Quantization)與基於百分位的量化(Percentile-based Quantization)。
一、對稱量化 (Symmetric Quantization)
對稱量化使用單個縮放因子(scale)將浮點數映射到對稱的整數範圍,以8位量化為例,範圍是[-127, 127]。以下為其核心公式與示意圖,其中: Xq 是量化後的值、Xf 是原始浮點數、s 是縮放因子、α 是數據的絕對最大值、n 是目標位數。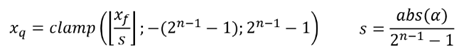
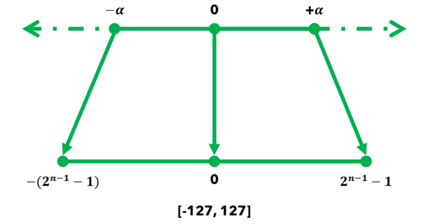
以下為對稱量化之程式與其輸出結果: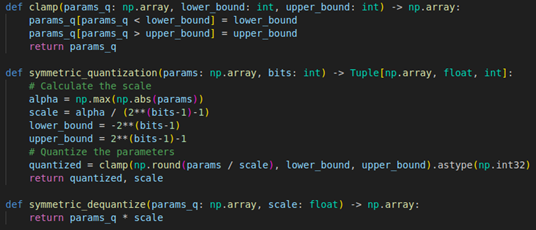
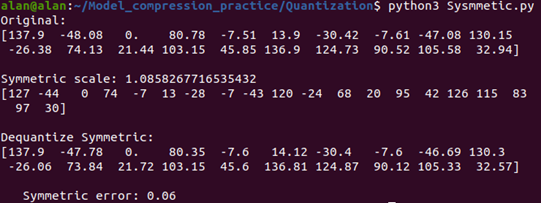
首先,實現了三個核心功能:值域限制(clamp)、量化(quantization)和解量化(dequantization)。當我們輸入一組包含正負值的浮點數據時,比如最大值137.9和最小值-48.08,程式會計算出最大絕對值137.9,然後將其除以127(8位元的最大正值)得到縮放因子1.0858,這個縮放因子的選擇確保了原始數據可以被完整地映射到量化範圍內。可以看到最大值137.9被量化為127,解量化後完美還原為137.9,最小值-48.08量化為-44,而解量化後變為-47.78,誤差僅0.3,零值完美保持,量化和解量化後仍為0,且這個量化過程產生的均方誤差(MSE)僅為0.06。
二、非對稱量化 (Asymmetric Quantization)
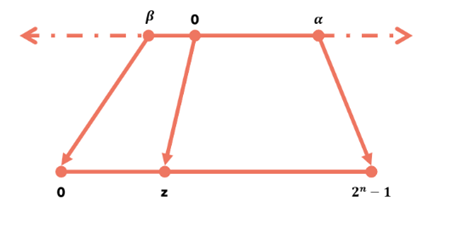
非對稱量化引入了零點(zero point)概念,使用縮放因子和零點兩個參數將浮點數映射到[0, 255]範圍。以下為其核心公式與示意圖,其中: z 是零點值、α 是最大值、β 是最小值、Xq 是量化後的值、Xf 是原始浮點數、s 是縮放因子。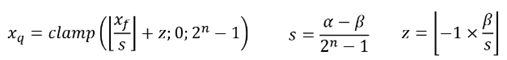
 以下為非對稱量化之程式與其輸出結果:
以下為非對稱量化之程式與其輸出結果:
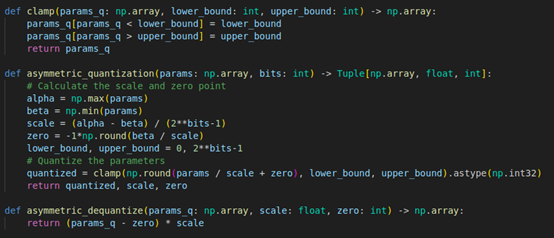
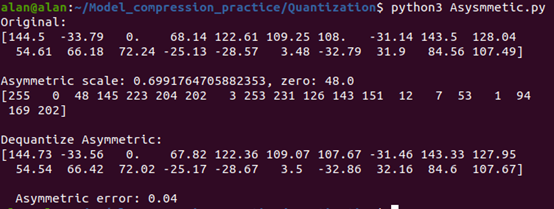
首先,一樣實現了三個核心功能:值域限制(clamp)、量化(quantization)和解量化(dequantization)。當我們輸入一組包含正負值的浮點數據時,比如最大值144.5和最小值-33.79,程式會計算出數據範圍(144.5減去-33.79),然後將其除以255(8位元的範圍)得到縮放因子0.699,同時計算出零點值48.0,這種設計確保了原始數據可以被完整地映射到[0, 255]的量化範圍內。可以看到最大值144.5被量化為255,解量化後變為144.73,誤差僅0.23,最小值-33.79量化為0,解量化後變為-33.56,誤差也僅0.23。最後,零值通過零點映射機制被量化為48,解量化後完美還原為0,且量化過程產生的均方誤差(MSE)僅為0.04,也展示了不錯的精度表現。
三、基於百分位的量化 (Percentile-based Quantization)
基於百分位的量化是非對稱量化的改進版本,同樣使用縮放因子和零點兩個參數將浮點數映射到[0, 255]範圍,但其特別之處在於使用百分位數來確定量化範圍,而不是直接使用最大最小值,其中:α是數據的99.99百分位數值、β是數據的0.01百分位數值、z是零點值、Xq是量化後的值、Xf是原始浮點數、s是縮放因子。
以下為百分位量化之程式與其輸出結果:
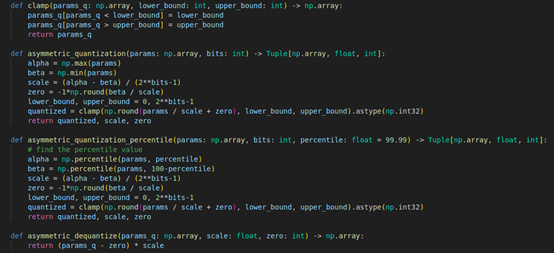
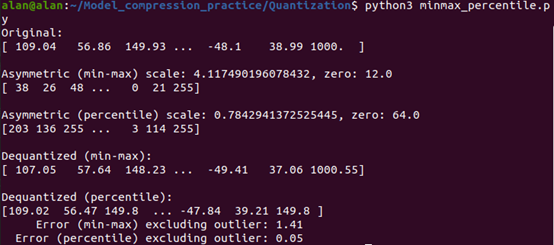
首先,一樣實現了三個核心功能:值域限制(clamp)、量化(quantization)和解量化(dequantization)。當我們輸入一組含有異常值的浮點數據時,比如數據主要分布在[-48.1, 149.93]範圍內,但存在一個異常值1000.0,程式會先計算出99.99百分位的數據範圍(不含異常值),然後將其除以255(8位元的範圍)得到縮放因子0.784,同時計算出零點值64.0,這種設計確保了主要數據可以被完整地映射到[0, 255]的量化範圍內,同時避免了異常值對量化精度的影響。可以看到正常範圍內的數值都得到了良好的量化效果,而異常值1000.0被限制在量化範圍內。特別是在不考慮異常值的情況下,這個量化過程產生的均方誤差(MSE)僅為0.05,比直接使用最大最小值進行量化的誤差1.41要小得多,展現了百分位量化在處理含異常值數據時的優勢。
四、三種方法之比較
這些特性使得三種方法各具優勢:對稱量化適合處理權重等對稱分布數據,非對稱量化適合處理偏斜分布的激活值,而百分位量化則在處理含噪聲或異常值的數據時表現優異。因此,實際應用時應根據數據特徵選擇合適的量化策略。
小結
透過以上講解與搭配程式碼進行說明,相信各位對各量化方法能有更深刻的理解,期待下一篇博文吧!
Q&A
問題一:為什麼非對稱量化需要引入零點(zero point)參數,而對稱量化不需要?
對稱量化使用[-127, 127]的範圍,自然有一個零點位置,且非對稱量化使用[0, 255]的範圍,需要零點來標記原始數據中的0值位置。
問題二:在實際應用中,如何選擇使用對稱量化還是非對稱量化?
如果數據呈對稱分布(如權重)或計算資源限制,使用對稱量化;而如果數據分布偏斜(如激活值)或計算資源充足,則使用非對稱量化。
問題三:為什麼在實驗中一些看似相近的數值,量化後的誤差會不同?
量化誤差的差異主要來自以下原因: 量化級別的分布和範圍邊界效應,如接近量化範圍邊界的值更容易受到限制,或是中間範圍的值通常有更好的精度。
問題四:在處理大規模深度學習模型時,非對稱量化的zero point會帶來什麼樣的記憶體和計算開銷?
這個問題涉及實際部署時的效能考慮,對於大型模型,可能需要儲存成千上萬個zero point值,因此對於相似分布的層,可以共用zero point,或是在硬體支援的情況下,可以使用SIMD指令加速運算。
問題五:在設計一個需要處理多種不同類型數據的深度學習模型時,如何為不同層選擇最適合的量化方法?
從模型整體架構來看,不同層的量化策略也需要有所調整。在模型的輸入層,建議使用百分位量化來處理可能的輸入噪聲;在中間的卷積層,可以對權重使用對稱量化,對激活值使用非對稱量化;在全連接層則可以組合使用對稱量化(如權重)和非對稱量化(如輸出)。
參考資料
[1] 對稱量化和非對稱量化 : 簡單的例子說明
評論