什麼是標準化?
特徵標準化(normalization)是將特徵資料按比例縮放,讓資料落在某一特定的區間。
為什麼要標準化?
當特徵做標準化有它的優點,除了可以優化梯度下降法外,還可以提高精準度。有的分類器需要計算樣本間的距離,例如一個特徵值的範圍非常大,那麼距離計算通常就會取決於這個特徵,若情況是範圍小的特徵比較重要的話,就會與我們所要的結果是相反的。資料標準化問題是資料探勘中特徵向量表達時的重要問題,當不同的特徵成列在一起的時候,由於特徵本身表達方式的原因而導致在絕對數值上的小資料被大資料“吃掉”的情況,這個時候我們需要做的就是對抽取出來的features vector進行標準化處理,以保證每個特徵被分類器平等對待。
以下介紹幾種標準化的方式:
1、(0,1)標準化:
這是最簡單也是最容易想到的方法,通過全部的feature vector裡的每一個數據,將Max和Min的記錄下來,並通過Max-Min作為基數(即Min=0,Max=1)進行數據的標準化處理:

圖1 (0,1)標準化
找大小的方法直接用np.max()和np.min()就行了。
2、Z-score標準化:
這種方法給予原始數據的均值(mean)和標準差(standard deviation)進行數據的標準化。經過處理的數據符合標準正態分佈,即均值為0,標準差為1
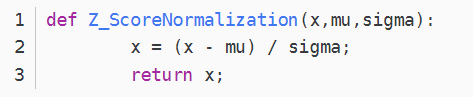
圖2 Z-score標準化
這裡mu(即均值)用np.average(),sigma(即標準差)用np.std()即可。
3、Sigmoid函數
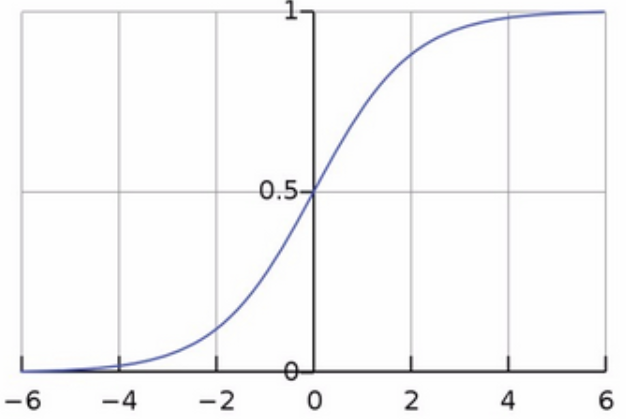
圖3 Sigmoid函數
Sigmoid函數是一個具有S形曲線的函數,是良好的閾值函數,在(0, 0.5)處中心對稱,在(0, 0.5)附近有比較大的斜率,而當數據趨向於正無窮和負無窮的時候,映射出來的值就會無限趨向於1和0,根據公式的改變,就可以改變分割閾值,這裡作為標準化方法,只考慮(0, 0.5)作為分割閾值的點的情況。
評論